Home
Favourites
Contact
Blog
Hindu Reviews
Q & A

Download App

Search Questions

Search

ट्रेन P उसकी विपरीत दिशा में आ रही ट्रेन Q को 45 सेकंड में पूरी तरह से पार कर जाती है। ट्रेन P और ट्रेन Q की लंबाइयाँ क्रमश: 1200 m और 1500 m है। ट्रेन Q की चाल 144 km/h है। ट्रेन P, 1800 m लंबे एक प्लेटफॉर्म को कितने समय में पार करेगी ?

Depth below the ground surface is c-Φ soil, where active earth pressure intensity is zero, is given by: किसी c-Φ मृदा में जमीन की सतह के नीचे जहाँ सक्रिय भूदाब तीव्रता शून्य है, उसकी गहराई निम्न द्वारा व्यक्त की जाती है-

निम्नलिखित में कौन-सी संसदीय लोकतंत्र की एक आवश्यक संस्था नहीं है?

आईसीसी पुरुष U19 क्रिकेट विश्व कप 2024 का आयोजन किस देश में किया जायेगा?

Gun metal contains 2 percent of– गन मेटल में 2 प्रतिशत ............... मिला होता है।

A question followed by two/three statement. Identify which statement is sufficient/necessary to answer the question. 34. You are given a question and four statements, decide which statement is sufficient to answer the question. There are 10 balls of different sizes and colors, green, yellow, blue, red and pink. Balls of same color are same in size. Can you find the sequence of largest to smallest Balls. Statement : 1) 3 red balls are larger than 2 green balls. 2) There are 2 pink balls which are smallest. 3) Two blue balls are largest. 4) Green is larger than yellow.

टाइप-A (IS-3406 – 1986) वाले काउंटर सिंक को सीट देने के लिए आप किस कोण वाले काउंटर सिंक ड्रिल का चयन करेंगे –

He is the best and popular actor of Bollywood

निम्नलिखित गद्यांश को पढ़कर पूछे गए प्रश्नों (प्रश्न सं. 16 से 23 तक) के सबसे उपयुक्त उत्तरवाले विकल्प को चिह्नित कीजिए– सुप्रसिद्ध गीतकार गोपालदास ‘नीरज’ ने अपनी एक रचना में कहा है– जैसा हो आघात रे वैसा बजे सितार तेरी ही आवाज की प्रतिध्वनि है संसार। हम वाद्ययंत्रों पर जैसा आघात करते हैं वैसी ही ध्वनि उनसे निकलती है। यदि कठोरता से आघात करते हैं तो कठोर ध्वनि उत्पन्न होती है, लेकिन यदि कोमलता से आघात करते हैं तो कर्णप्रिय कोमल ध्वनि उत्पन्न होती है। यदि हम किसी वाद्ययंत्र को नियमपूर्वक ठीक से बजाते हैं तो सही राग उत्पन्न होता है, अन्यथा सही राग उत्पन्न होने का प्रश्न ही नहीं उठता। सही राग उत्पन्न न होने की स्थिति में गुणीजन हमारे गायन अथवा वादन की ओर आकर्षित ही नहीं होंगे। हमारे जीवन रूपी सितार की भी वही स्थिति होती है। यदि हम अनुशासन में रहते हुए प्रत्येक कार्य नियमानुसार करते हैं तो जीवन रूपी सितार से उत्पन्न होने वाला प्रत्येक राग रूपी कार्य हमें सार्थकता और आनंद ही प्रदान करेगा। इस संसार में हम जो कुछ सोचते, कहते अथवा करते हैं वही हमारे पास लौटकर आता है। न कम, न अधिक। जब हम किसी खंडहर अथवा वादी में कोई अच्छा शब्द या वाक्य बोलते हैं तो कुछ देर बाद वही अच्छा शब्द या वाक्य गूँजता हुआ हमें सुनाई पड़ता है और यदि हम कोई बुरा, अपमानजनक अथवा घृणास्पद शब्द या वाक्य बोलते हैं तो कुछ देर बाद वही बुरा, अपमानजनक अथवा घृणास्पद शब्द या वाक्य हमें सुनाई पड़ता है। यदि हम सुरीली आवाज निकालते हैं तो वैसी ही सुरीली आवाज लौट कर हमारे पास आती है, लेकिन यदि हम डरावनी आवाज निकालते हैं तो वैसी ही डरावनी आवाज लौटकर आती है। हम जैसा एक बार बोलते हैं वैसा ही कई बार सुनने को अभिशप्त होते हैं। पर यह बात अनुभव करते हुए भी इसका आशय हम समझते नहीं। चूँकि आवाज के लौटकर आने में थोड़ा वक्त लगता है, इसलिए हम उसे स्वतंत्र घटना मान लेते हैं। यह अहसास नहीं कर पाते कि हमारे ही किए हुए काज, हमारे ही सोचे हुए भाव अलग दिशा से हमारे पास आते दिख रहे हैं। ‘कर्णप्रिय’ ध्वनि का आशय है–

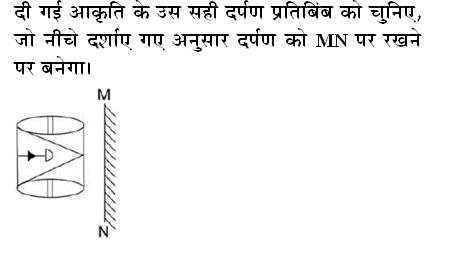
Q: N is a whole number which when, divided by 6 leaves the remainder 4. Find the remainder when 2N is divided by 6.

A. 4

B. 8

C. 2

D. Zero

Correct Answer: Option C - Let the quotient be “a” when N is divided by 6. ∴ N = 6a + 4……….(i) By equation (i) ×2, 2N = 2 × 6a + 8 2N = 12a + 6 + 2 2N = 6 (2a +1) + 2 Hence, the required remainder will be 2.

C. Let the quotient be “a” when N is divided by 6. ∴ N = 6a + 4……….(i) By equation (i) ×2, 2N = 2 × 6a + 8 2N = 12a + 6 + 2 2N = 6 (2a +1) + 2 Hence, the required remainder will be 2.

Explanations:

Let the quotient be “a” when N is divided by 6. ∴ N = 6a + 4……….(i) By equation (i) ×2, 2N = 2 × 6a + 8 2N = 12a + 6 + 2 2N = 6 (2a +1) + 2 Hence, the required remainder will be 2.

Download Our App

Download our app to know more Lorem ipsum dolor sit amet consectetur adipisicing elit. Excepturi, esse.

YOU ARE NOT LOGIN

Unlocking possibilities: Login required for a world of personalized experiences.

Address

12, Church Ln, The Adelphi, Allen Ganj, Prayagraj, Uttar Pradesh 211002

+91 9554973128

Address

info.yctbooks@gmail.com

Link's

Home

Favourites

Contact

Download Our App