Q: If tan3θ.tan7θ = 1, where 7θ is an acute angle, then find the value of cot15θ
-
A.
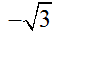
- B. 1
- C. -1
-
D.
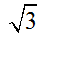
Correct Answer:
Option C - tan3θ.tan7θ = 1 (where7θ is an acute angle)
tan7θ = cot3θ
tan7θ = tan(90° – 3θ)
7θ= 90° – 3θ
then (3θ+7θ) = 90°
10θ = 90°
θ = 9°
then cot 15θ
cot (15 x 9)°
= cot 135°
= cot (90x1+45°) = – tan 45°
= –1
C. tan3θ.tan7θ = 1 (where7θ is an acute angle)
tan7θ = cot3θ
tan7θ = tan(90° – 3θ)
7θ= 90° – 3θ
then (3θ+7θ) = 90°
10θ = 90°
θ = 9°
then cot 15θ
cot (15 x 9)°
= cot 135°
= cot (90x1+45°) = – tan 45°
= –1
Explanations:
tan3θ.tan7θ = 1 (where7θ is an acute angle) tan7θ = cot3θ tan7θ = tan(90° – 3θ) 7θ= 90° – 3θ then (3θ+7θ) = 90° 10θ = 90° θ = 9° then cot 15θ cot (15 x 9)° = cot 135° = cot (90x1+45°) = – tan 45° = –1

